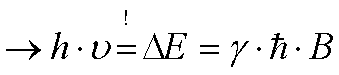Merke:
Zwei Oszillatoren koppeln am stärksten, wenn sie die gleiche Eigenfrequenz
besitzen.
Merke:
Zwei Oszillatoren koppeln am stärksten, wenn sie die gleiche Eigenfrequenz
besitzen.
→ RESONANZ
Viele Kerne besitzen einen Spindrehimpuls. Ein Kern mit der Spinquantenzahl I
hat einen Drehimpuls (L) von:
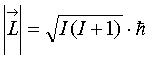 (Klassisch:
(Klassisch: 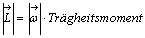 )
)
I kann halbzahlig oder ganzzahlig sein.
Besitzt ein Kern einen (Spin)Drehimpuls, so besitzt er wie alle bewegte Ladung
auch ein Magnetisches Moment (Kompassnadelmodell).
→ für I >0 besitzt der Kern einen Drehimpuls und somit ein magnetisches Moment
(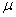 )
mit konstantem Betrag.
)
mit konstantem Betrag.
 Merke:
Die Kerne, welche man als häufigstes zur Strukturaufklärung mittels NMR
heranzieht, sind:
Merke:
Die Kerne, welche man als häufigstes zur Strukturaufklärung mittels NMR
heranzieht, sind:
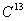 und
und
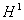 (also
Protonen). Sowohl C13 wie auch H haben eine
Spinquantenzahl von ½ = I.
(also
Protonen). Sowohl C13 wie auch H haben eine
Spinquantenzahl von ½ = I.
 (Kerne
mit gerader Zahl von Protonen und gerader Zahl von Neutronen haben I = 0 → sie
besitzen kein magnetisches Moment [z.B. C12, O16].
Folglich sind sie im NMR Spektrum unsichtbar, wie später erläutert wird.)
(Kerne
mit gerader Zahl von Protonen und gerader Zahl von Neutronen haben I = 0 → sie
besitzen kein magnetisches Moment [z.B. C12, O16].
Folglich sind sie im NMR Spektrum unsichtbar, wie später erläutert wird.)
Wird Materie in ein Homogenes Magnetfeld gebracht, so richten sich die Kerne wie
kleine Kompassnadeln im Magnetfeld aus. Da Energie in Mikroskopischen
Größenordnungen nur gequantelt vorkommt, kann das Magnetische Moment im Raum
lediglich 2I+1 Orientierungen einnehmen. (folgt aus quantentheoretischen
Überlegungen)
Das magnetische Moment eines Kerns ist Proportional zu seinem Drehimpuls!
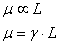
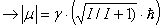
Der Proportionalitätsfaktor 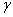 wird
gyroskopisches Verhältnis genannt. Das Magnetische Moment eines Kerns ist eine
Eigenschaft des Kernes selbst und nicht von außen Beeinflussbar.
wird
gyroskopisches Verhältnis genannt. Das Magnetische Moment eines Kerns ist eine
Eigenschaft des Kernes selbst und nicht von außen Beeinflussbar.
Für Spin ½ Kerne:
(da I = ½ Kerne mit abstand die wichtigsten sind wird im weiteren Text
ausschließlich auf jene eingegangen)
Das Magnetische Moment eines Kerns kann lediglich
2I+1 = 2 Orientierungen im Raum
einnehmen:

Entweder μ+ in Richtung des Magnetfeldes (energieärmer) oder einmal μ- (höhere
Energie) entgegen das von außen angelegte statische Magnetfeld. μz
bezeichnet die Komponente von μ in Z-Richtung. Sie berechnet sich bei I= 1/2
Kernen zu +1/2γħ und -1/2γħ.
Obwohl μ+ Energieärmer ist als μ- werden beide zustände im Thermodynamischen
Gleichgewicht (maximale Entropie) fast gleichmäßig besetzt, da
die Energiedifferenz sehr klein ist. μ+ wird oft auch als α Zustand und μ- als β
Zustand bezeichnet. Da der α Zustand energetisch leicht begünstigt ist ist die
Wahrscheinlichkeit, dass ein Kern im β zustand vorliegt nur 0.99995 mal so groß
wie der α Zustand (Bolzmannverteilung).
Mit anderen Worten: Die "Stoffmenge" n(β-Kernen) = 0,99995* n(α-Kernen).
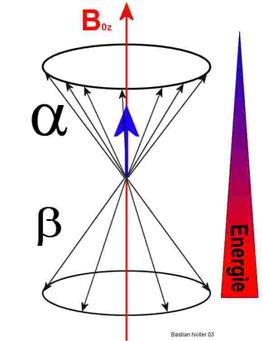
Folglich ergibt sich eine Makroskopische Magnetisierung (M0), als
Summe aller magnetischen Momente, in Z-Richtung:
 Im
Thermodynamischen Gleichgewicht
Im
Thermodynamischen Gleichgewicht
Blau eingezeichnet ist die Makroskopische Magnetisierung (M0), welche
aus der Summe aller Magnetischer Momente der Kerne in der Materie, aufgrund des
von außen angelegten B0z-Feldes, resultiert. Ohne das Äußere Feld
könnten sich die Kernspins willkürlich im Raum anordnen. Auf Grund der
Quantenbedingung können sie im Feld nur zwei Orientierungen einnehmen. Wobei
hierbei α Orientierung leicht begünstigt ist.
Hierbei rotieren (präzessieren) die Magnetischen Momente der Kerne mit einer
ganz bestimmten Frequenz um die Z-Achse. Diese Frequenz heißt Lamorfrequenz.

Merke: Grundlage aller Spektroskopischen Methoden ist die Wechselwirkung
von Materie mit elektromagnetischen wellen.
Damit eine WW eintritt, muss eine Anregung von einem energetisch niedrigen
Niveau in ein energetisch höheres Niveau stattfinden. Diese Energiedifferenz
muss genau der Energiequanten der EM-Strahlung entsprechen. Die Energie der
Zustände Alpha und Beta berechnet sich zu:
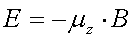
Folglich beträgt die Energie des Alpha Zustandes 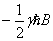 und
die Energie des Beta Zustandes
und
die Energie des Beta Zustandes 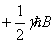 .
.
Der Energieunterschied zwischen den beiden Niveaus ist also proportional zum
lokalen Magnetfeld am Kern (B):
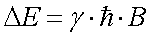

Merke: Damit ein Übergang (Anregung) stattfindet, muss ein Energiequant von 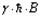 in
form von EM-Strahlung eingestrahlt werden.
in
form von EM-Strahlung eingestrahlt werden.
→RESONANZBEDINGUNG der NMR bei
Spin 1/2 Kernen:
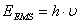
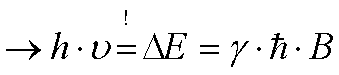
→ Je Stärker das angelegte Magnetfeld, desto
größer ist die Aufspaltung und desto größer muss die Frequenz der eingestrahlten
Wellen ausfallen.
Außerdem gilt:

Die Larmorfrequenz (Frequenz mit der die
magnetischen Momente der Kerne präzessieren) ist gleich der Frequenz der
eingestrahlten EM-Strahlung. Die Larmorfrequenz ist damit ebenfalls proportional
zur Magnetfeldstärke am Kern.

Merke: Ist die Resonanzbedingung erfüllt, tritt eine Starke Kopplung
zwischen den Kernspins und dem elektromagnetischen Feld ein. → Starke Absorption
der Strahlung → Kerne werden in das höhere Energieniveau gehoben
und fangen an synchron zu präzessieren.
→ Auslenkung der Makroskopischen Magnetisierung (M0) aus
Richtung Bz . Jene präzessiert mit der Larmorfrequenz weiter und
induziert eine Spannung in der Spule (Empfänger) des NMR Gerätes:

Der Grüne Pfeil soll die Bewegung von M0 verdeutlichen. Das mit
der Larmorfrequenz ( = Resonanzfrequenz) rotierende Makroskopische magnetische
Moment Induziert in einer Spule eine Wechselspannung, welche logischerweise mit
der der gleiche Frequenz oszilliert und das eigentlich NMR Signal darstellt.
Wäre das Magnetfeld an jedem Wasserstoffatom gleich, so hätten alle H-Atome die
Gleiche Resonanzfrequenz.
Zum glück ist das ist das magnetische Feld am Kernort nicht nur abhängig
vom außen angelegten Feld, sondern auch von der Kernumgebung sprich von der Lage
im Molekül. Somit haben chemisch nicht äquivalent H-Atome unterschiedliche
Resonanzfrequenzen. Diese Tatsache macht man sich zur Strukturaufklärung von
Molekülen zunutze.
Der Aufbau eines NMR-Gerätes:
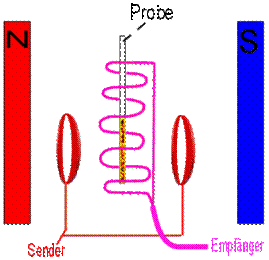
Es ergeben sich nun zwei Möglichkeiten einen Kern in Resonanz zu versetzen und
damit Rückschlüsse auf seine molekulare Umgebung erhalten.
1.) Frequenzsweep:
→ kontinuierliche Änderung der Sendefrequenz (υ) bei konstantem äußeren
Feld (B0 = konst.) bis Resonanz.
2.) Feldsweep:
→ kontinuierliche Änderung der magnetischen Flussdichte (B0) des
außen angelegten Feldes bei konstanter Sendefrequenz bis Resonanz.
Beide Methoden sind allerdings schon veraltet. Es ist sehr zeitaufwendig ein
komplettes Spektrum zu durchlaufen.
Deshalb hat sich die Fourier-Impuls-NMR etabliert, welche viel schneller
durchzuführen ist. Somit können von einer Probe gleich mehrere Spektren
hintereinander aufgenommen werden und deren Amplituden aufaddiert werden. Dies
führt zu einem erheblich besseren Signal/Rausch Verhältniss.
Bei der Methode wird das Äußere Magnetfeld konstant gehalten. Und gleich ein
ganzes Spektrum an EM-Strahlung eingesendet. Somit werden alle Kerne
gleichzeitig angeregt. Als Signal erhält man eine Überlagerung aller
Resonanzfrequenzen der unterschiedlichen Kernen. Dieses Überlagerte Signal wird
mit einem Computer mit Hilfe der mathematischen Fourier-Transform-Methode in die
Einzelsignale zerlegt.

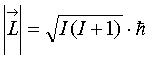 (Klassisch:
(Klassisch: